Q1. Two different types of rubber are found to have the stress-strain curves shown below in the figure below.
 (i) In which significant ways do these curves differ from the stress-strain curve of a metal wire.
(ii) A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers A and B would you prefer to use for this purpose? Why?
(iii) Which of the two rubber materials would you choose for a car tyre?
(i) In which significant ways do these curves differ from the stress-strain curve of a metal wire.
(ii) A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers A and B would you prefer to use for this purpose? Why?
(iii) Which of the two rubber materials would you choose for a car tyre?
 (i) In which significant ways do these curves differ from the stress-strain curve of a metal wire.
(ii) A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers A and B would you prefer to use for this purpose? Why?
(iii) Which of the two rubber materials would you choose for a car tyre?
(i) In which significant ways do these curves differ from the stress-strain curve of a metal wire.
(ii) A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers A and B would you prefer to use for this purpose? Why?
(iii) Which of the two rubber materials would you choose for a car tyre?
Solution
(i) The curves differ as regards the following points :
(a) The linear portions of the curves being smaller, Hooke's law is not obeyed even for small stress.
(b) There is no permanent strain even for large stresses.
(c) The elastic region is larger in the present curves.
(d) During unloading, the same curve is not retraced in the present case.
(ii) We should use rubber B to absorb vibrations of the machinery. It is because of larger area of the curve that greater amount of vibrational energy can be dissipated.
(iii) We should use rubber A for making car tyres. Because the work done in case rubber A is lesser (lesser area of the curve), hence the car tyres of this rubber will not get excessively heated.
Q2. Which type of substances are called elastomers? Give one example.
Solution
Those materials for which stress vs strain variation is not a straight line within elastic limit are called elastomers. e.g. Rubber, tissue of aorta.
Q3. A sphere of radius 10 cm is subjected to a pressure of 100 atm. Its volume decreases by 0.2 cc. Find its Bulk modulus.
Solution
Radius of sphere = 10 cm
Change in volume,  = 0.2 cc
Pressure on the sphere = 100 atm = 1.013 x 106 dyne cm-2
We know that,
= 0.2 cc
Pressure on the sphere = 100 atm = 1.013 x 106 dyne cm-2
We know that,

 = 0.2 cc
Pressure on the sphere = 100 atm = 1.013 x 106 dyne cm-2
We know that,
= 0.2 cc
Pressure on the sphere = 100 atm = 1.013 x 106 dyne cm-2
We know that,

Q4. (a) Define Young's modulus of a material.
(b) Define Bulk modulus of a body.
Solution
(a) The ratio of the tensile stress to the longitudinal strain is called Young's modulus. It is denoted by Y in honour of Thomas Young.
(b) The ratio of hydraulic stress to the corresponding hydraulic strain is defined as the bulk modulus and is denoted by K.
Q5. What do you mean by the elastic limit?
Solution
When the deforming force is increased, a limit is reached beyond which if the applied force is removed, the solid does not come back to its original shape or size but remains deformed. This limit is called the elastic limit.
Q6. Which is more elastic, steel or rubber? why?
Solution
Steel is more elastic than rubber, because the inter-atomic bonding strength is more in steel than that in rubber.
Q7. Plot stress vs strain curve for a metal. On the graph depict:
(i) Yield point (ii) Fracture point (iii) Proportional limit (iv) Permanent set.
Solution
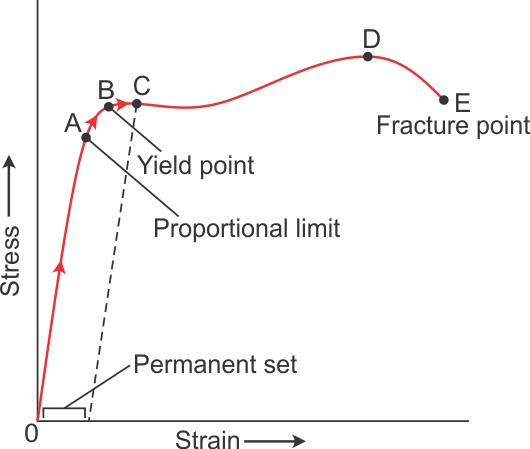
Q8. Two wires A and B are of the same material. Their lengths are in the ratio 1 : 2 and the diameters in the ratio 2 : 1. If they are pulled by the same force, what will be the ratio of their increase in lengths?
Solution
We know that,
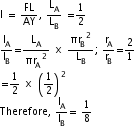
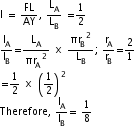
Q9. (a) How does Young's modulus change with the rise of temperature?
(b) Is water more elastic than air? Why?
Solution
(a) It decreases with rise in temperature.
(b) Yes. water is more elastic than air. It is because air is more compressible than water, and volume elasticity is reciprocal of compressibility.
Q10. A wire 50 cm long and 1 sq.mm is cross-section has the Young's modulus, Y = 2 x 1010Nm-2. How much work is done in stretching the wire through 1 mm?
Solution
Y = 2 x 1010Nm-2, L = 50cm = 0.5 m, A = 1 mm2 = 10-6m2
Extension,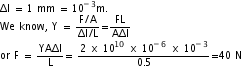 Work done in stretching the wire = Average force x Extension
=
Work done in stretching the wire = Average force x Extension
= 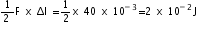
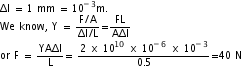 Work done in stretching the wire = Average force x Extension
=
Work done in stretching the wire = Average force x Extension
= 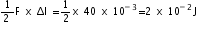
Q11. A metal cube of side 10 cm is subjected to a shearing stress of 106 Nm-2. Calculate the modulus of rigidity if the top of the cube is displaced by 0.05 cm with respect to its bottom.
Solution
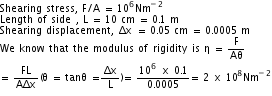
Comments
Post a Comment