Q1. Anil uses an electric motor of 2 h.p. What is its power in watts? And what is the amount of work done by the motor in pulling water in one minute.
Solution
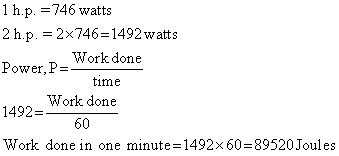
Q2. What is difference between head-on and an oblique collision?
Solution
Head-on collision- A collision is said to be head-on collision when the colliding objects move along a straight line joining their centres.
Oblique Collision- When the colliding objects do not move along the straight line joining their centres, the collision is said to be oblique collision.
Q3. A skater starts from rest on a frictionless hill with vertical height of 50 m and an inclination of 30o. Calculate how far the skater can go horizontally after he reaches the bottom of the hill, if the coefficient of the kinetic friction between the skis and snow is 0.21.
Solution
From the law of mechanical conservation of energy, we have
 Now, the distance covered by the skater is equal to the change its kinetic energy and this is equal to the work done by the frictional force.
Thus,
Now, the distance covered by the skater is equal to the change its kinetic energy and this is equal to the work done by the frictional force.
Thus,
 So, the skater would cover a horizontal distance of 238.36 m after reaching the bottom of the hill.
So, the skater would cover a horizontal distance of 238.36 m after reaching the bottom of the hill.
 Now, the distance covered by the skater is equal to the change its kinetic energy and this is equal to the work done by the frictional force.
Thus,
Now, the distance covered by the skater is equal to the change its kinetic energy and this is equal to the work done by the frictional force.
Thus,
 So, the skater would cover a horizontal distance of 238.36 m after reaching the bottom of the hill.
So, the skater would cover a horizontal distance of 238.36 m after reaching the bottom of the hill.
Q4. A body constrained to move along the z-axis of a coordinate system is subjected to a constant force F given by
 where
where  are unit vectors along the x, y and z-axis of the system respectively. What is the work done by this force in moving the body through a distance of 4 m along the z-axis?
are unit vectors along the x, y and z-axis of the system respectively. What is the work done by this force in moving the body through a distance of 4 m along the z-axis?
 where
where  are unit vectors along the x, y and z-axis of the system respectively. What is the work done by this force in moving the body through a distance of 4 m along the z-axis?
are unit vectors along the x, y and z-axis of the system respectively. What is the work done by this force in moving the body through a distance of 4 m along the z-axis?Solution

Q5. There are two balls each of mass M moving in opposite directions with equal speeds u undergo a head-on collision. Calculate velocity of the two balls after collision?
Solution
Here we are given that
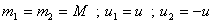
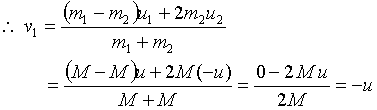
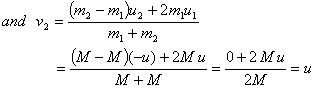 Thus after collision, the two balls bounce back with equal speeds.
Thus after collision, the two balls bounce back with equal speeds.
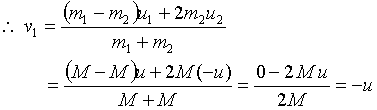
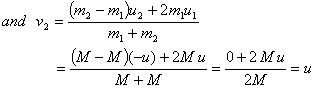 Thus after collision, the two balls bounce back with equal speeds.
Thus after collision, the two balls bounce back with equal speeds.
Q6. Predict the sign of the work done in the following cases:-(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket. (b) work done by gravitational force in the above case (a).(c) work done by friction on a body sliding down an inclined plane. (d) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Solution
(a) Since tension in the rope is in the same direction as displacement, work done is positive.(b) Work done is negative since gravitational force acts downwards, while displacement is upwards.(c) Since friction opposes motion down the plane, it is directed opposite to displacement. Therefore work is negative.(d) Work done by resistive force of air is negative because this force opposes motion.
Q7. A particle moves along y axis. How does the kinetic energy of the particle change when its velocity changes from -4 m/s to -2m/s? What is the sign of the work done?
Solution
Here we are given
Final velocity is v = -2 m/s
Initial velocity is u = -4 m/s
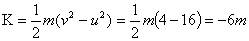 So its kinetic energy decreases. The particle slows down.
Since W = ? K, the sign of work done is negative.
So its kinetic energy decreases. The particle slows down.
Since W = ? K, the sign of work done is negative.
Q8. A 120 g mass has a velocity of  =
=  ms-1 at a certain instant. What is its K. E?
ms-1 at a certain instant. What is its K. E?
 =
=  ms-1 at a certain instant. What is its K. E?
ms-1 at a certain instant. What is its K. E?Solution
K.E =  mv2
=
mv2
= m
m  =
=  m
m  .
.  =
=  x
x  (4 + 25) J
= 1.74J
(4 + 25) J
= 1.74J
 mv2
=
mv2
= m
m  =
=  m
m  .
.  =
=  x
x  (4 + 25) J
= 1.74J
(4 + 25) J
= 1.74J
Q9. What is h.p.? What is the relation between h.p. and watts?
Solution
Horse power is a unit to measure power.
1 h.p. = 746 watts
Q10. Prove that the initial downward velocity of a ball is  when it is thrown from a height of h metres such that it hits the ground and loses half of its energy and bounces back to the same height.
when it is thrown from a height of h metres such that it hits the ground and loses half of its energy and bounces back to the same height.
 when it is thrown from a height of h metres such that it hits the ground and loses half of its energy and bounces back to the same height.
when it is thrown from a height of h metres such that it hits the ground and loses half of its energy and bounces back to the same height.Solution
Let the potential energy of the ball be = mgh
It is given that initial velocity of ball = v0
Therefore, total energy at the time of throwing the ball
=  And, the energy after collision with ground
=
And, the energy after collision with ground
=  As the ball again rises to height h, we have
As the ball again rises to height h, we have
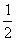
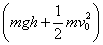 =
=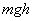 or
or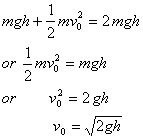 Hence Proved.
Hence Proved.
 And, the energy after collision with ground
=
And, the energy after collision with ground
=  As the ball again rises to height h, we have
As the ball again rises to height h, we have
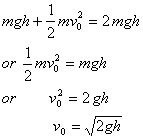 Hence Proved.
Hence Proved.
Q11. Calculate the velocity of the bob of simple pendulum at its mean position if it is able to rise to vertical height of 20 cm. Take g = 9.8 m/s2.
Solution
Kinetic energy of the bob at the mean position = Potential energy of the bob at the highest position.
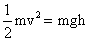
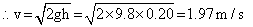
Q12. A body falling from the height of 10 m rebounds from the hard surface. It loses 20% of its energy in impact. What is the height to which it would raise after the impact and where this energy goes after hitting the surface?
Solution
Let the potential energy of the body at height 10 m be mgh.
Let the potential energy after striking the surface be mgh'.
After striking the surface, it loses 20% of its energy.
Thus, its new potential energy is (100 - 20)% mgh = 80% mgh
Now, we have
 The energy is dissipated as heat after hitting the surface.
The energy is dissipated as heat after hitting the surface.
 The energy is dissipated as heat after hitting the surface.
The energy is dissipated as heat after hitting the surface.
Q13. A body is moving with the speed of 30 m/s. How high can it be lifted to gain an amount of potential energy equal to its kinetic energy. (Take g = 10 m/s2)
Solution
Kinetic energy of the body  Potential energy of the body = mgh
Now, it is given that potential energy is equal to its kinetic energy at height say 'h'.
Potential energy of the body = mgh
Now, it is given that potential energy is equal to its kinetic energy at height say 'h'.

 Potential energy of the body = mgh
Now, it is given that potential energy is equal to its kinetic energy at height say 'h'.
Potential energy of the body = mgh
Now, it is given that potential energy is equal to its kinetic energy at height say 'h'.

Q14. State and prove work energy theorem.
Solution
Work energy theorem states that the change in kinetic energy of an object is equal to the net work done on it by the net force.
Let us suppose that a body is initially at rest and a force  is applied on the body to displace it through
is applied on the body to displace it through 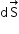 along the direction of the force. Then, small amount of work done is given by
along the direction of the force. Then, small amount of work done is given by
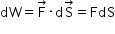 Also, according to Newton's second law of motion, we have
Also, according to Newton's second law of motion, we have
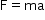 where a is acceleration produced (in the direction of force) on applying the force. Therefore,
where a is acceleration produced (in the direction of force) on applying the force. Therefore,
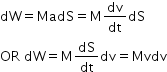 Now, work done by the force in order to increase its velocity from u (initial velocity) to v (final velocity) is given by
Now, work done by the force in order to increase its velocity from u (initial velocity) to v (final velocity) is given by
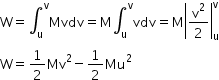 Hence, work done on a body by a force is equal to the change in its kinetic energy.
Hence, work done on a body by a force is equal to the change in its kinetic energy.
 is applied on the body to displace it through
is applied on the body to displace it through 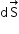 along the direction of the force. Then, small amount of work done is given by
along the direction of the force. Then, small amount of work done is given by
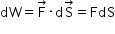 Also, according to Newton's second law of motion, we have
Also, according to Newton's second law of motion, we have
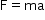 where a is acceleration produced (in the direction of force) on applying the force. Therefore,
where a is acceleration produced (in the direction of force) on applying the force. Therefore,
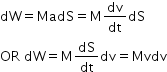 Now, work done by the force in order to increase its velocity from u (initial velocity) to v (final velocity) is given by
Now, work done by the force in order to increase its velocity from u (initial velocity) to v (final velocity) is given by
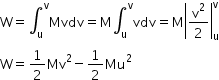 Hence, work done on a body by a force is equal to the change in its kinetic energy.
Hence, work done on a body by a force is equal to the change in its kinetic energy.
Q15. A body of mass m is released in vaccum from the position A at a height h above the ground.Prove that sum of kinetic and potential energies A, B and C remains constant.


Solution
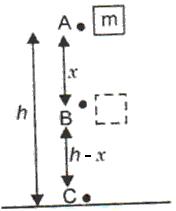
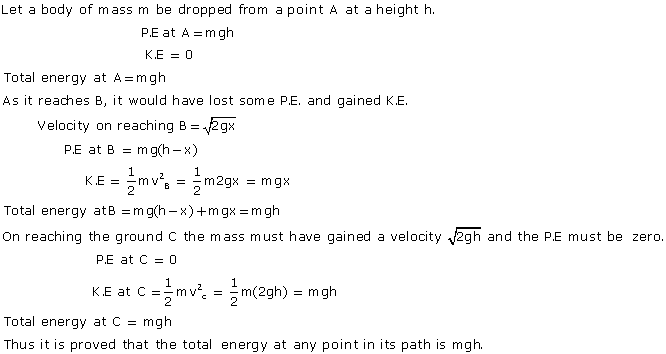
Q16. A mass of 30 kg moving with a speed of 20 m/s collides with another stationary mass of 10 kg. As a result of collision, the two mass stick together. What will be the kinetic energy of composite mass?
Solution
Let v be the velocity of composite mass
Momentum after collision = (30+10) v
Momentum before collision = 30 × 20 + 10 × 0
Applying principle of conservation of momentum, we have
(30+10) v = 30 × 20 + 10 × 0
40 v = 600
or v = 15 m/s
Now, kinetic energy is given as


Q17. Aman and Aryan lift 50 Kg dumbbell over their head through same distance. Aman lifts it 10 times in 1 minute whereas Aryan lifts it 10 times in 10 seconds. Who does more work and who has more power?
Solution

Q18. A delivery boy of mass 58 kg runs up 50 steps in 40 seconds to reach the counter. If the height of each step is 15 cm, calculate his power.
Solution

Q19. A bullet of mass m moving with a horizontal velocity v strikes a stationary block of mass M suspended by a string of length L. The bullet gets embedded in the block. What is the maximum angle made by the string after the impact?
Solution
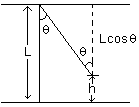 From the geometry of the above figure it is clear that the height h reached can be expressed in terms of length of the string and the angle made.
When the bullet gets embedded in the block, then h = L - L cos θ ------ (1)
Applying law of conservation of momentum, we have
Mass of bullet times its velocity before collision = sum of masses of bullet and block times velocity of block
mv = (m + M) V ------- (2) Where V is the velocity of block and bullet after the impact.
Also, from the law of conservation of energy, we have
From the geometry of the above figure it is clear that the height h reached can be expressed in terms of length of the string and the angle made.
When the bullet gets embedded in the block, then h = L - L cos θ ------ (1)
Applying law of conservation of momentum, we have
Mass of bullet times its velocity before collision = sum of masses of bullet and block times velocity of block
mv = (m + M) V ------- (2) Where V is the velocity of block and bullet after the impact.
Also, from the law of conservation of energy, we have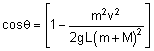
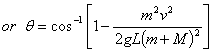
Q20. A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance by which the trunk has been moved is 20 m. Plot the force applied by the woman and the frictional force, which is 50 N. Calculate the work done by the two forces over 20 m.
Solution
Let us plot a force-displacement graph for the force applied by the woman 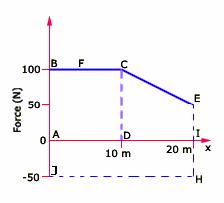 The plot of the applied force is shown in figure.
At x = 20 m, F = 50 N (
The plot of the applied force is shown in figure.
At x = 20 m, F = 50 N ( 0). We are given that the frictional force f=50 N. It opposes motion and acts in a direction opposite to F. It is therefore shown on the negative side of the force axis.The work done by the woman is WF = area of the rectangle ABCD + area of the trapezium CEID.
0). We are given that the frictional force f=50 N. It opposes motion and acts in a direction opposite to F. It is therefore shown on the negative side of the force axis.The work done by the woman is WF = area of the rectangle ABCD + area of the trapezium CEID.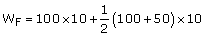 = 1000 + 750 = 1750 JThe work done by the frictional force is W = area of the rectangle AIHJ = -50 ×20 = -1000 J
The area on the negative side of the force axis has negative sign.
= 1000 + 750 = 1750 JThe work done by the frictional force is W = area of the rectangle AIHJ = -50 ×20 = -1000 J
The area on the negative side of the force axis has negative sign.
 The plot of the applied force is shown in figure.
At x = 20 m, F = 50 N (
The plot of the applied force is shown in figure.
At x = 20 m, F = 50 N (
Q21. A ball of mass 0.1 kg is thrown vertically up with a velocity of 10 m/s. At what height, will its kinetic energy be half its original value?
Solution
Work done against gravitational force = change in K.E
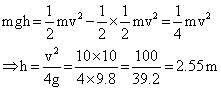
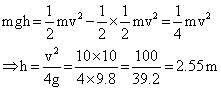
Q22. A block of mass 1 kg initially at rest is dropped from the height of 1 m onto a vertical spring having force constant 400 Nm-1. Calculate the maximum distance through which the spring will be compressed.
Solution
Let the spring be compressed through distance x. Then, the block falls through a height of (h + x).
Potential energy of falling block decreases and that of vertical spring increases due to compression. So, increase in potential energy of spring = Loss in potential energy of the block
 The maximum distance through which spring compressed is 0.2450 m.
The maximum distance through which spring compressed is 0.2450 m.
 The maximum distance through which spring compressed is 0.2450 m.
The maximum distance through which spring compressed is 0.2450 m.
Q23. A ball at rest is dropped from a height of 10 m. It loses 25% of its kinetic energy in striking the ground. Find the height to which it bounces. Give the reason of loss of kinetic energy.
Solution
Potential energy lost by the ball = Kinetic energy gained by the ball = mgh
On bouncing upward, the ball lost 25% of its kinetic energy and remaining 75% changes back to potential energy.
Let the ball bounce back to height h', then
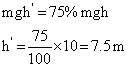 The loss in kinetic energy of the ball is due to the heat produced by air friction.
The loss in kinetic energy of the ball is due to the heat produced by air friction.
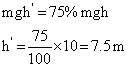 The loss in kinetic energy of the ball is due to the heat produced by air friction.
The loss in kinetic energy of the ball is due to the heat produced by air friction.
Q24. An airplane with a mass of 2000 kg sinks 1000 metres moving forward a horizontal distance of 10,000 metres. What will be its new potential energy? (Take g = 10 m/s2)
Solution
Mass of the airplane is m = 2000 kg
Decrease in height (sinks) is h = 1000 m
Distance covered = 10,000 metres
So by the potential energy relation, the change in the gravitational potential energy of the airplane
= m x g x h.
Thus, the new potential energy is
2000 x (10) x (1000) = 2 x 107 J
Q25. Derive equation for loss of kinetic energy in case of a completely inelastic collision in one dimension?
Solution
Consider two masses m1 and m2. Let the particle m1 be moving with initial speed v1i and m2 be at rest.
 In case of an perfectly inelastic collision in one dimension,
In case of an perfectly inelastic collision in one dimension, 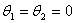 Applying law of conservation of momentum, we get
Applying law of conservation of momentum, we get
 where vf is the final velocity of the combined mass (m1+m2)
The loss in kinetic energy on collision is
where vf is the final velocity of the combined mass (m1+m2)
The loss in kinetic energy on collision is
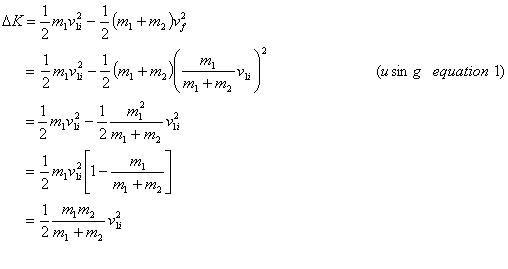 The above quantity is a positive quantity.
The above quantity is a positive quantity.
 In case of an perfectly inelastic collision in one dimension,
In case of an perfectly inelastic collision in one dimension,  where vf is the final velocity of the combined mass (m1+m2)
The loss in kinetic energy on collision is
where vf is the final velocity of the combined mass (m1+m2)
The loss in kinetic energy on collision is
 The above quantity is a positive quantity.
The above quantity is a positive quantity.
Q26. What is the value of coefficient of restitution for a perfectly plastic body and why?
Solution
The value of coefficient of restitution for a perfectly plastic body is zero, because the two colliding bodies stick together.
Comments
Post a Comment