Q1. What do you mean by banking of a curved road and banking angle?
Solution
Raising the outer edge of a curved road above its inner edge is called banking of a curved road.
The angle through which the outer edge of the curved road is raised above the inner edge is called angle of banking.
Q2. Two blocks of different masses are pushed along the frictionless surface at an angle. Draw the free body diagram of both the blocks and of the system. And also mention the forces acting on them separately. 

Solution
Free body diagram for block A:
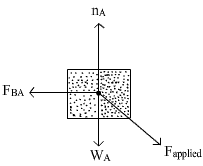 Forces on block A are:
(i) WA = Weight of the block, acting downward.
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) Fapplied = Applied force
(iv) FBA = Force exerted on A by the block B.
Free body diagram for block B:
Forces on block A are:
(i) WA = Weight of the block, acting downward.
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) Fapplied = Applied force
(iv) FBA = Force exerted on A by the block B.
Free body diagram for block B:
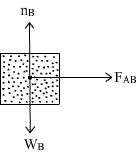 Forces on block B are:
(i) WA = Weight of the block, acting downward.
(i) nA = Normal reaction force, acting vertically upward.
(ii) FAB = Force exerted by A on B.
Free body diagram for the system of both blocks:
Forces on block B are:
(i) WA = Weight of the block, acting downward.
(i) nA = Normal reaction force, acting vertically upward.
(ii) FAB = Force exerted by A on B.
Free body diagram for the system of both blocks:
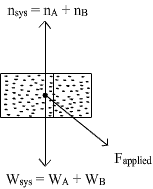 Resultant forces on both the system are:
(i) nsystem = Total reaction force from the surface.
(ii) Wsystem = Total weight of the system, acting downward.
(iii) Fapplied = Applied force
Resultant forces on both the system are:
(i) nsystem = Total reaction force from the surface.
(ii) Wsystem = Total weight of the system, acting downward.
(iii) Fapplied = Applied force
 Forces on block A are:
(i) WA = Weight of the block, acting downward.
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) Fapplied = Applied force
(iv) FBA = Force exerted on A by the block B.
Free body diagram for block B:
Forces on block A are:
(i) WA = Weight of the block, acting downward.
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) Fapplied = Applied force
(iv) FBA = Force exerted on A by the block B.
Free body diagram for block B:
 Forces on block B are:
(i) WA = Weight of the block, acting downward.
(i) nA = Normal reaction force, acting vertically upward.
(ii) FAB = Force exerted by A on B.
Free body diagram for the system of both blocks:
Forces on block B are:
(i) WA = Weight of the block, acting downward.
(i) nA = Normal reaction force, acting vertically upward.
(ii) FAB = Force exerted by A on B.
Free body diagram for the system of both blocks:
 Resultant forces on both the system are:
(i) nsystem = Total reaction force from the surface.
(ii) Wsystem = Total weight of the system, acting downward.
(iii) Fapplied = Applied force
Resultant forces on both the system are:
(i) nsystem = Total reaction force from the surface.
(ii) Wsystem = Total weight of the system, acting downward.
(iii) Fapplied = Applied force
Q3. A mass of 8 kg is suspended by a rope of length 4 m from the ceiling. A force of 40 N in the horizontal direction is applied at the midpoint P of the rope, as shown in the figure below. What angle does the rope make with the vertical in equilibrium? 

Solution
From the figure, we have
T2 = 8 × 10 = 80 N
Now, considering the equilibrium of the point P under the action of three forces, T1, T2
and horizontal force 40 N, the horizontal and vertical components of the resultant forces
must vanish separately.
T1cos θ = T2 = 80 N
T1 sin θ = 40 N
By dividing the above two equations, we get


Q4. Which force provides the necessary centripetal force to the planets to move in circular orbit around the sun?
Solution
Gravitational force between sun and the planets provides the necessary centripetal force for the planets to move in circular orbit.
Q5. A block of mass M is placed on a rough horizontal surface. A force F = mg acts on the block. If this force is inclined at an angle θ, then considering the coefficient of friction μ find the relation between θ and μ.
Solution
Block can be pulled only when the horizontal component of force is greater than the force of friction. The vertical component of force will decrease the weight and the normal reaction.
So, we get the condition


Q6. Explain briefly: (a) Static Friction (b) Kinetic friction
Solution
1. Static Friction
Static friction is the force between two objects that are not moving relative to each other. When there is no applied force, there is no static friction. It comes into play the moment there is an applied force.
Static frictional forces arise from the interlocking of the irregularities of two surfaces which prevent any relative motion until some limiting value of force is applied.
It is found experimentally that, the limiting value of static friction  is independent of the area of contact and varies with the normal force (N) approximately as:
is independent of the area of contact and varies with the normal force (N) approximately as:
 where
where  is a constant of proportionality depending only on the nature of the surfaces in contact. The constant
is a constant of proportionality depending only on the nature of the surfaces in contact. The constant  is called the coefficient of static friction.
2. Kinetic Friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground).
Kinetic friction, like static friction, is found to be independent of the area of contact. Further, it is nearly independent of the velocity. It satisfies a law similar to that for static friction:
is called the coefficient of static friction.
2. Kinetic Friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground).
Kinetic friction, like static friction, is found to be independent of the area of contact. Further, it is nearly independent of the velocity. It satisfies a law similar to that for static friction:
 where
where  the coefficient of kinetic friction, depends only on the surfaces in contact.
the coefficient of kinetic friction, depends only on the surfaces in contact.
 is independent of the area of contact and varies with the normal force (N) approximately as:
is independent of the area of contact and varies with the normal force (N) approximately as:
 where
where  is a constant of proportionality depending only on the nature of the surfaces in contact. The constant
is a constant of proportionality depending only on the nature of the surfaces in contact. The constant  is called the coefficient of static friction.
2. Kinetic Friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground).
Kinetic friction, like static friction, is found to be independent of the area of contact. Further, it is nearly independent of the velocity. It satisfies a law similar to that for static friction:
is called the coefficient of static friction.
2. Kinetic Friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground).
Kinetic friction, like static friction, is found to be independent of the area of contact. Further, it is nearly independent of the velocity. It satisfies a law similar to that for static friction:
 where
where  the coefficient of kinetic friction, depends only on the surfaces in contact.
the coefficient of kinetic friction, depends only on the surfaces in contact.
Q7. Determine the acceleration of the car in which a box lying on its floor will remain stationary, given that the co-efficient of static friction between the box and the train's floor is 0.25.
Solution

Q8. A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 30 N, when the lift is stationary. What will be the reading of the spring balance, if the lift moves downward with an acceleration of 5 ms-2.
Solution
When the lift is stationary:
The reaction is equal to the weight of the man, that is
R = Mg = 30 N
Therefore, M = 30/g = 30/9.8 = 3.06
When the lift is moving:
Let R1be the reaction, when the lift is moving with an acceleration a = 5 ms-2 in the downward direction.
Then, we have
R1= M (g-a) = 3.06 × (9.8 - 5) = 14.7 ≈ 15 N
Q9. A girl pulls a loaded sledge of mass 100 kg along a horizontal surface at constant velocity in snow. The coefficient of kinetic friction between girl and the snow is 0.10. Draw its free body diagram and calculate tension in the string. Given Φ = 45o.
Solution
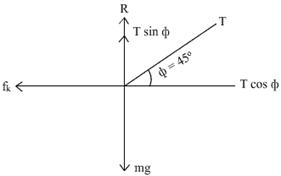

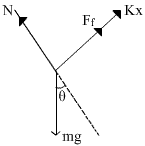
Q10. Draw a free body diagram of a block of mass m attached to a spring of constant k on a rough incline at angle θ. 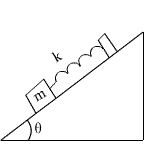

Solution
The forces experienced by blocks are
Weight = mg
Normal force due to incline = N
Friction force = Ff
Spring force = kx

Q11. A 20 gram bullet moving with 200 m/s stops after penetrating a 2 cm of bone. Calculate the average force exerted by the bullet.
Solution
Here we are given,
Mass of the bullet = 20 g = 20 × 10-3 kg
Initial velocity of the bullet is u = 200 m/s
Distance traveled = 2 cm = 2 × 10-2 m
Using 3rd equation of motion, we get

 From Newton's second law, we have
From Newton's second law, we have


 From Newton's second law, we have
From Newton's second law, we have

Q12. A man in a circus jumps from a height of 20 m and is caught by a net spread below him. The net sags down 3 m due to this impact. Calculate the average force exerted by the net on the man to stop his fall. Take the mass to be 50 kg and consider the value of acceleration during his free fall as 10 m/s2.
Solution
Let v be the final velocity with which the man touches the net, after falling through a height of 20 m.
Thus, using Newton's second equation of motion as
 Hence, the man touches the net with a velocity of 20 m/s.
At the same time, he experiences a net upward force by the net and the velocity goes on decreasing and finally becomes zero after he drops by a height of 3 m.
So, here we have, u = 20 m/s; v = 0; S = 3 m
Using Newton's second equation of motion as
Hence, the man touches the net with a velocity of 20 m/s.
At the same time, he experiences a net upward force by the net and the velocity goes on decreasing and finally becomes zero after he drops by a height of 3 m.
So, here we have, u = 20 m/s; v = 0; S = 3 m
Using Newton's second equation of motion as
 Therefore, the average retarding force = mass of the man x retardation = 50 x 66.6 = 3330 N.
Therefore, the average retarding force = mass of the man x retardation = 50 x 66.6 = 3330 N.
 Hence, the man touches the net with a velocity of 20 m/s.
At the same time, he experiences a net upward force by the net and the velocity goes on decreasing and finally becomes zero after he drops by a height of 3 m.
So, here we have, u = 20 m/s; v = 0; S = 3 m
Using Newton's second equation of motion as
Hence, the man touches the net with a velocity of 20 m/s.
At the same time, he experiences a net upward force by the net and the velocity goes on decreasing and finally becomes zero after he drops by a height of 3 m.
So, here we have, u = 20 m/s; v = 0; S = 3 m
Using Newton's second equation of motion as
 Therefore, the average retarding force = mass of the man x retardation = 50 x 66.6 = 3330 N.
Therefore, the average retarding force = mass of the man x retardation = 50 x 66.6 = 3330 N.
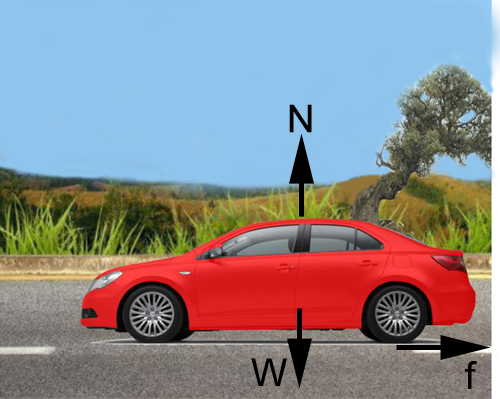
Q13. Which three forces act on a vehicle during the motion on a level road?
Solution
(i) The weight of the car, mg in the downward direction.
(ii) Normal Reaction, N in the upward direction.
(iii) Frictional Force, f in the direction opposite to the direction of motion.

Q14. Free body diagram of three situations are shown below. The net force is known for each situation. However, the magnitude of few of the forces is not known. Determine the magnitude of the unknown forces. 

Solution
Force on A = 60 N and on B = 100 N, as the net force on the object is zero.
Now, in second object, the net force on the object is 700 N. So the force on C = 800 N.
In the third situation, the apposite forces D and F cancel out. As the net force on the object is 30 N towards right, and hence the force on E will be 70 N.
Q15. A gardener is mowing a lawn by pushing and pulling the machine. In which condition is the normal force highest?
Solution
Normal force depends on the weight. Higher the weight, higher is the normal force. So, while pushing, the gardener will put more effort and hence increasing the weight leading to higher normal reaction.
Q16. What were the views of Greek philosopher Aristotle about the state of motion?
Solution
According to Aristotle's law of motion, an external force is necessary to keep a body in motion. However, Aristotle was proved to be wrong by Galileo. It was observed that the external forces were necessary to counter the opposing forces of friction to keep bodies in uniform motion. If there were no friction, no external force would be needed to maintain the state of uniform motion.
Q17. What is the need of banking a circular road?
Solution
When a circular road is banked, the horizontal component of the normal reaction of the road provides the necessary centripetal force for the vehicle to move it along the curved path.
Q18. Give two examples in which force can be exerted on the body without making any contact with them.
Solution
(1) A ball released from the top of a building accelerates downward due to the gravitational pull of the earth.
(2) A bar magnet can attract an iron nail from a distance.
Q19. Why are the passengers thrown forward when a speeding bus stops suddenly?
Solution
This is due to inertia. When the speeding bus stops suddenly, lower part of the body comes to rest while the upper part of the body tends to maintain uniform motion. Hence, the passenger’s are thrown forward.
Q20. Three blocks of different masses are placed one over other on a horizontal surface. Draw the free body diagram for each block separately.


Solution
Force on block C:
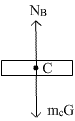 (i) mC g = weight of block C, acting downward (ii) NB = Normal reaction from B
Force on block B:
(i) mC g = weight of block C, acting downward (ii) NB = Normal reaction from B
Force on block B:
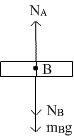 (i) mB g = weight of block B, acting downward
(ii) NA = Normal reaction from upper surface of A
(iii) NB = Normal reaction from lower surface of C on B, acting downward
Force on block A:
(i) mB g = weight of block B, acting downward
(ii) NA = Normal reaction from upper surface of A
(iii) NB = Normal reaction from lower surface of C on B, acting downward
Force on block A:
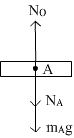 (i) mA g = weight of block A, acting downward
(ii) No = Normal reaction from horizontal surface
(iii) NA = Normal reaction from lower surface B, acting downward
(i) mA g = weight of block A, acting downward
(ii) No = Normal reaction from horizontal surface
(iii) NA = Normal reaction from lower surface B, acting downward
 (i) mC g = weight of block C, acting downward (ii) NB = Normal reaction from B
Force on block B:
(i) mC g = weight of block C, acting downward (ii) NB = Normal reaction from B
Force on block B:
 (i) mB g = weight of block B, acting downward
(ii) NA = Normal reaction from upper surface of A
(iii) NB = Normal reaction from lower surface of C on B, acting downward
Force on block A:
(i) mB g = weight of block B, acting downward
(ii) NA = Normal reaction from upper surface of A
(iii) NB = Normal reaction from lower surface of C on B, acting downward
Force on block A:
 (i) mA g = weight of block A, acting downward
(ii) No = Normal reaction from horizontal surface
(iii) NA = Normal reaction from lower surface B, acting downward
(i) mA g = weight of block A, acting downward
(ii) No = Normal reaction from horizontal surface
(iii) NA = Normal reaction from lower surface B, acting downward
Q21. Give the formula of Spring Force and state the significance of the negative sign.
Solution
Spring Force F = - k x
k --> Spring Constant
x --> Displacement
The formula has a negative sign indicating that the restoring force will act in the direction opposite to the displacement.
Q22. A force of 60 dyne is inclined to the horizontal at an angle of 60°. Find the acceleration in a mass of 6 g, which moves in the horizontal direction.
Solution
Here, M = 6 g
F = 60 dyne and is inclined at an angle 600 with the horizontal.
 Component of force along the horizontal is
Component of force along the horizontal is
 If a is acceleration along the horizontal, then
If a is acceleration along the horizontal, then

 Component of force along the horizontal is
Component of force along the horizontal is
 If a is acceleration along the horizontal, then
If a is acceleration along the horizontal, then

Q23. Explain why a stone thrown on a glass window smashes the window pane into pieces, but a bullet from the gun passes through making a clean hole.
Solution
The velocity of stone is much less than that of the bullet fired from a gun. Due to its low speed the stone remains in contact with the window pane for a longer time and hence motion is shared by whole of the window pane.
On the other hand, the bullet fired from gun, remains in contact with the window pane for such a small time that it shares its motion only with a portion of the window pane. That's why it makes a clean hole in the window pane.
Q24. A tractor tows a trailer of mass 1000 kg at a speed of 10 m/s. On level road the tension in the string is 1000 N. Find the tension in the coupling when the tractor ascends a road having inclination of 1 in 5.
Solution
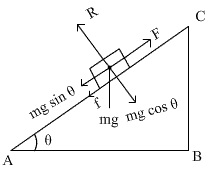 On a level road, force applied by the truck is equal to the friction that it overcomes.
f = 1000 N
When a tractor ascends the road of inclination 1 in 5 (that is,
On a level road, force applied by the truck is equal to the friction that it overcomes.
f = 1000 N
When a tractor ascends the road of inclination 1 in 5 (that is,  ), it overcomes frictional force and the component of the weight of the trailer.
So, the tension in the coupling is
), it overcomes frictional force and the component of the weight of the trailer.
So, the tension in the coupling is

Q25. A 1 kg ball falls from a height of 5 m and rebounds to a height of 1.5 m.Find the change in linear momentum and average force between the ball and the ground, if the time during which they are in contact is 0.1 s. Take g = 10 m/s2.
Solution
The force diagram for the problem is
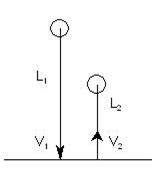 The object falls from a height h1 = 5 m and rebounds to height h2 = 1.5 m.
If v1 is the velocity with which the ball hits the ground, then we have
The object falls from a height h1 = 5 m and rebounds to height h2 = 1.5 m.
If v1 is the velocity with which the ball hits the ground, then we have
 If v2 is the velocity of the ball just after rebound at the ground, then we have after the rebound of the ball
If v2 is the velocity of the ball just after rebound at the ground, then we have after the rebound of the ball
 Here v'2 is the final velocity of the ball at the maximum height.
But,
Here v'2 is the final velocity of the ball at the maximum height.
But,
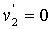
 Now, the change in linear momentum is
Now, the change in linear momentum is
 We know that
We know that
 Where Δt = 0.1 second is the time for which the ball remained in contact with the ground during the collision.
Where Δt = 0.1 second is the time for which the ball remained in contact with the ground during the collision.
 The object falls from a height h1 = 5 m and rebounds to height h2 = 1.5 m.
If v1 is the velocity with which the ball hits the ground, then we have
The object falls from a height h1 = 5 m and rebounds to height h2 = 1.5 m.
If v1 is the velocity with which the ball hits the ground, then we have
 If v2 is the velocity of the ball just after rebound at the ground, then we have after the rebound of the ball
If v2 is the velocity of the ball just after rebound at the ground, then we have after the rebound of the ball
 Here v'2 is the final velocity of the ball at the maximum height.
But,
Here v'2 is the final velocity of the ball at the maximum height.
But,
 Now, the change in linear momentum is
Now, the change in linear momentum is
 We know that
We know that
 Where Δt = 0.1 second is the time for which the ball remained in contact with the ground during the collision.
Where Δt = 0.1 second is the time for which the ball remained in contact with the ground during the collision.
Q26. A ball of mass 1.5 kg lying on floor when given a velocity of 5 m/s gets stopped due to friction in 10 s. Calculate the coefficient of friction. Given g = 10 m/s2.
Solution
We know that
Initial velocity is u = 5 m/s
Final velocity is v = 0 (as the ball gets stopped)
Time is t = 10 s
According to the equations of motion, we have


Q27. A weighing machine inside a stationary lift reads 50 kgf, when a man stands on it. What would happen to the weighing machine reading, if the lift is moving with constant velocity and constant acceleration?
Solution
Apparent weight, W' = m(g + a), where a is the acceleration with which the lift moves upwards.
(1) When the lift moves with constant velocity, a = 0
Therefore, W' = m(g + 0) = mg = 50 kgf (weight remains the same)
(2) When the lift moves with the acceleration a in the upward direction, we have
W' = m (g + a)  50 kgf
Hence, the apparent weight will increase if the lift will move with acceleration a.
50 kgf
Hence, the apparent weight will increase if the lift will move with acceleration a.
Q28. Why do we beat a blanket with a stick to remove dust particles?
Solution
When we beat blanket with stick it comes into motion. But, the dust particles remain at rest due to inertia and get detached from the blanket.
Q29. Why does gun recoil while firing?
Solution
When a gun is fired, the force of the gas produced by burning gunpowder hurls out of the bullet. Hence, in accordance with the Newton's third law of motion, the gun itself recoils backwards, i.e., in the opposite direction of the bullet.
Q30. The three blocks of mass 4 kg, 5 kg, and 6 kg are suspended with the string, which is passed over a pulley. Calculate the tension T1, T2, and T3 when the whole system is moving with an acceleration of 5 m/s2. 

Solution
When the system is moving in the upward direction with acceleration 5 m/s2
T1 - (m1 + m2 + m3) g = (m1 + m2 + m3) a
T1 = (m1 + m2 + m3) (a + g)
T1 = (4 + 5 + 6) × (5 + 9.8) = 222 N
Consider the free body diagram of block of mass m2 and m3.
T2 - (m2 + m3) g = (m2 + m3) a
T2 = (m2 + m3) (a + g)
T2 = (5 + 6) (5 + 9.8) = 162.8 N
Considering the free body diagram of mass m3
T3 - m3 g = m3 a
T3 = m3 (a + g)
T3 = 6 × 14.8 = 88.8 N
Q31. A circular track of radius 100 m is banked at an angle of 30°. If the coefficient of friction between the wheels of a car and the road is 0.5, then what is the (i) optimum speed of the car to avoid wear and tear on its tires, and (ii) maximum permissible speed to avoid slipping?
Solution
Radius R = 100 m, θ = 30o, μ = 0.5
At the optimum speed, the normal reaction's component is enough to provide the needed centripetal force, and the frictional force is not needed. So, the optimum speed is given by
 The maximum permissible speed is given by
The maximum permissible speed is given by

 The maximum permissible speed is given by
The maximum permissible speed is given by

Q32. Why is a hammer used to drive a nail into wood?
Solution
A heavy hammer imparts large momentum, due to its large mass. Hence it is preferred to use a hammer while driving nail into wood.
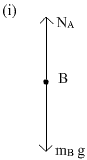
Q33. Draw free body diagram of two blocks placed one over other as shown in figure.


Solution
Force on box B are
(i) mBg = WB = its weight, acting downward
(ii) NA = normal force on B due to upper surface of block A, acting upward.
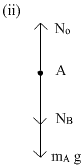
 Force on box A are
(i) mAg = WA = its weight, acting downward
(ii) No = normal force on A due to horizontal surface, acting upward.
(iii) NB = normal force on A due to lower surface of block B acting downward.
Force on box A are
(i) mAg = WA = its weight, acting downward
(ii) No = normal force on A due to horizontal surface, acting upward.
(iii) NB = normal force on A due to lower surface of block B acting downward.
 Force on box A are
(i) mAg = WA = its weight, acting downward
(ii) No = normal force on A due to horizontal surface, acting upward.
(iii) NB = normal force on A due to lower surface of block B acting downward.
Force on box A are
(i) mAg = WA = its weight, acting downward
(ii) No = normal force on A due to horizontal surface, acting upward.
(iii) NB = normal force on A due to lower surface of block B acting downward.

Q34. When a ball is thrown up in a moving train, it comes back to the person's hands instead of falling backwards. Why?
Solution
During its upward and downward motion, the ball continues to move with the same horizontal velocity as the train. In this period, the ball covers the same horizontal distance as the train and so it comes back to the hands of the person throwing it.
Q35. A man is driving a car with a speed of 36 km/hr (roughly 10 m/s). Suddenly a child appears in the middle of the road. He slams on the brakes, which in turn exerts a retarding force of 1000 N. The mass of the man and the car together is 500 kg. If the child is 27 metres away from the car when he first hit the brakes, will the child be saved?
Solution
Total mass of driver + car = m = 500 kg
Initial velocity of the car is
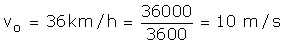 Final velocity is
Final velocity is
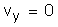 Average retarding force is F = -1000 N.
From Newton's 2nd law, we have
Average retarding force is F = -1000 N.
From Newton's 2nd law, we have
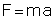 So, the acceleration is
So, the acceleration is
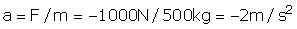 Now, using the equation of kinematics, we find the stopping distance d as
Now, using the equation of kinematics, we find the stopping distance d as
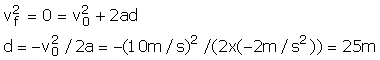 Thus, the child is saved as it was at a distance of 27 m.
Thus, the child is saved as it was at a distance of 27 m.
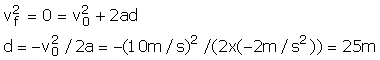 Thus, the child is saved as it was at a distance of 27 m.
Thus, the child is saved as it was at a distance of 27 m.
Q36. Two wooden blocks A and B are connected to a chord, passing through a frictionless pulley. Block A is pushed to the left on a surface by a horizontal force. Draw the free body diagram of both the blocks.

Solution
Free body diagram of block A:
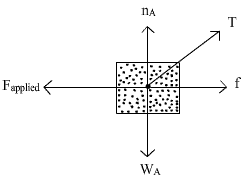 Forces on block A are:
(i) WA = Weight of the block, acting downward
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) T = Tension of chord
(iv) Fapplied = Applied force
(v) f = Frictional force, acting against the applied force.
Free body diagram of Forces on block B is:
Forces on block A are:
(i) WA = Weight of the block, acting downward
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) T = Tension of chord
(iv) Fapplied = Applied force
(v) f = Frictional force, acting against the applied force.
Free body diagram of Forces on block B is:
 T = Tension in chord, acting vertically upward
WB = Weight of the body, acting vertically downward.
T = Tension in chord, acting vertically upward
WB = Weight of the body, acting vertically downward.
 Forces on block A are:
(i) WA = Weight of the block, acting downward
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) T = Tension of chord
(iv) Fapplied = Applied force
(v) f = Frictional force, acting against the applied force.
Free body diagram of Forces on block B is:
Forces on block A are:
(i) WA = Weight of the block, acting downward
(ii) nA = Normal reaction force from surface, acting vertically upward.
(iii) T = Tension of chord
(iv) Fapplied = Applied force
(v) f = Frictional force, acting against the applied force.
Free body diagram of Forces on block B is:
 T = Tension in chord, acting vertically upward
WB = Weight of the body, acting vertically downward.
T = Tension in chord, acting vertically upward
WB = Weight of the body, acting vertically downward.
Comments
Post a Comment