Q1. A tuning fork gives 3 beats per second with sonometer wire when its length is either 49.8 cm of 50.2 cm. Find the frequency of tuning fork.
Solution
Let v, v1 and v2 be the frequencies of tuning fork and sonometer wire when its length is 49.8 cm and 50.2 cm respectively. As frequency of sonometer wire is inversely proportional to length of the sonometer wire, therefore,
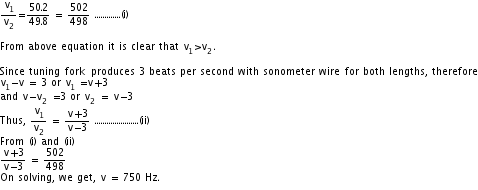
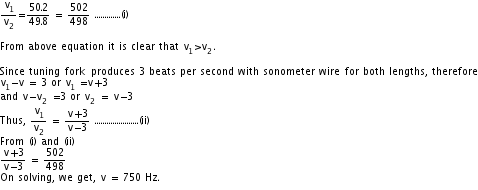
Q2. A bat emits ultrasonic sound of frequency 100 kHz in air. If this sound meets a water surface, what is the wavelength of (i) the reflected sound, (ii) the transmitted sound? Speed of sound in air = 340 ms-1 and in water = 1486 ms-1.
Solution
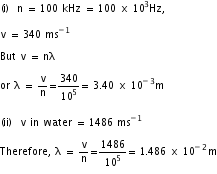
Q3. An engine approaches a high vertical wall with constant speed of 90 m/sec. When it is at a distance of 1050 m from the wall, it blows a whistle, whose echo is heard after 5 second. Calculate the speed of sound in air.
Solution
Let V be the velocity of sound and u be the velocity of source and echo is heard after time t. Let the engine whistle when it is at P and hear the echo at Q.
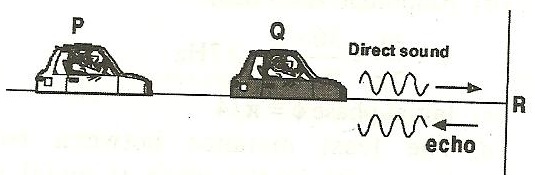 Therefore, Distance travelled by engine in time t.
PQ = ut .........................(i)
and the distance travelled sound in time t
PR + RQ = Vt .........................(ii)
Add (i) and (ii), we get PR + RQ + PQ = 2PR = (V + u)t
Here u = 90 m/s = (V + 90) x 5
5V = 1650 or V = 330 m/s
Therefore, Distance travelled by engine in time t.
PQ = ut .........................(i)
and the distance travelled sound in time t
PR + RQ = Vt .........................(ii)
Add (i) and (ii), we get PR + RQ + PQ = 2PR = (V + u)t
Here u = 90 m/s = (V + 90) x 5
5V = 1650 or V = 330 m/s
 Therefore, Distance travelled by engine in time t.
PQ = ut .........................(i)
and the distance travelled sound in time t
PR + RQ = Vt .........................(ii)
Add (i) and (ii), we get PR + RQ + PQ = 2PR = (V + u)t
Here u = 90 m/s = (V + 90) x 5
5V = 1650 or V = 330 m/s
Therefore, Distance travelled by engine in time t.
PQ = ut .........................(i)
and the distance travelled sound in time t
PR + RQ = Vt .........................(ii)
Add (i) and (ii), we get PR + RQ + PQ = 2PR = (V + u)t
Here u = 90 m/s = (V + 90) x 5
5V = 1650 or V = 330 m/s
Q4. Define longitudinal wave motion. What are the essential conditions required for the formation of longitudinal wave motion?
Solution
It is that wave motion in which the particles of the medium through which the wave is travelling vibrate in a direction parallel to the direction of the motion of the wave.
In the figure, the wave is travelling from left to right, and the particles of the medium vibrate in the horizontal direction simple harmonically. It represents the longitudinal wave motion.
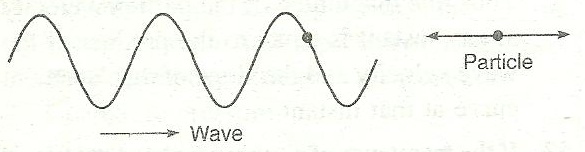 For their propagation, the medium must possess:
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
For their propagation, the medium must possess:
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
 For their propagation, the medium must possess:
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
For their propagation, the medium must possess:
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
Q5. A set of 28 tuning forks is arranged in a series of decreasing frequencies. The first tuning fork is higher ocatve of last tuning fork. When the two consecutive tuning forks are sound together, 4 beats are produced. Find the frequency of first and last tuning fork.
Solution
Let the frequency of last tuning fork is v. Thus the frequency of first tuning fork will be 2v. As the two successive tuning forks produce 4 beats, therefore the frequency of other tuning fork will be
2v, 2v-4, 2v-8.........................v.
The above series is AP series. For AP series we have
Tn = a + (n-1)d
Here Tn = v, a = 2v,
n = 28, d = -4
Therefore, v = 2v + (28 - 1) (-4)
or v = 108 Hz and 2v = 216 Hz
Q6. A resonance air column shows resonance with a fork of frequency n at lengths l1 and l2. Write down the formula of the speed of sound in air. What is the formula for end correction?
Solution

Q7. A train is moving on a straight track with speed 20 ms-1. It is blowing its whistle at the frequency of 1000 Hz. The percentage change in the frequency heard by a person standing near the track as the train passes him is (speed of sound = 320 ms-1) close to:
Solution
A train is moving on a straight track with speed vs = 20 m/s. It is blowing its whistle at the frequency of f0 = 1000 Hz.The frequency of the whistle heard by the person standing near the track is given as:
As the train approaches the person:
 As the train goes away from the person:
As the train goes away from the person:
 The percentage change in the frequency heard by the person standing near the track as the train passes him is given as:
The percentage change in the frequency heard by the person standing near the track as the train passes him is given as:
 Thus, the frequency heard by a person standing near the track changes by 12 % as the train passes him.
Thus, the frequency heard by a person standing near the track changes by 12 % as the train passes him.
 As the train goes away from the person:
As the train goes away from the person:
 The percentage change in the frequency heard by the person standing near the track as the train passes him is given as:
The percentage change in the frequency heard by the person standing near the track as the train passes him is given as:
 Thus, the frequency heard by a person standing near the track changes by 12 % as the train passes him.
Thus, the frequency heard by a person standing near the track changes by 12 % as the train passes him.
Q8. Show that the velocity of sound increases by 61 cm/s for every 1oC.
Solution
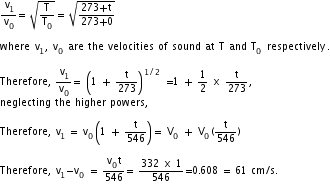 Thus, the velocity of sound increases by 61 cm/s for every 1oC ( or 1K) rise in the temperature.
Thus, the velocity of sound increases by 61 cm/s for every 1oC ( or 1K) rise in the temperature.
Q9. Write four points of difference between progressive waves and stationary waves.
Solution
Progressive waves :
1. The disturbance travels onward, it being handed over from one particle to the adjoining particle.
2. Energy is trasferred in thex medium along the waves.
3. The amplitude of vibration of each particle is the same.
4. No particle of the medium is permanently at rest.
Stationary waves :
1. The disturbance is confined to a particular region and there is no onward motion.
2. There is no transference of energy in the medium.
3. The amplitude of vibration of the particles changes from zero at nodes to maximum at antinodes.
4. The particles of the medium at nodes are permanently at rest.
Q10. Given below are some examples of wave-motion. State in each case if the wave-motion is transverse, longitudinal or a combination of both :
(i) Motion of a kink in a long coil spring produced by displacing the end of the spring sideways.
(ii) Waves produced in a cylinder containing a liquid by moving its piston back and forth.
(iii) Waves produced by a motor boat sailing in water.
(iv) Light waves travelling from the sun to the earth.
(v) Ultrasonic waves in air produced by a vibrating quartz crystal.
Solution
(i) Transverse, because the vibration of particles of the spring are at right angles to the direction of wave propagation.
(ii) Longitudinal, because the molecules of the liquid vibrate to and fro about their mean positions along the direction propagation of the wave.
(iii) Combination of transverse and longitudinal.
(iv) Transverse, because the light waves are electromagnetic waves in which electric and magnetic fields oscillate in the direction at right angles to each other and also to the direction of propagation of the wave.
(v) Longitudinal, because the direction of vibration of air molecules is to and fro about its mean position along the direction of propagation of wave due to the vibration of quartz crystal.
Q11. In an experiment it was found that a tuning fork and a sonometer gave 5 beats per second, both when the length of the wire was 1 m and 0.05 m. Calculate the frequency of the fork.
Solution
Let the frequency of the tuning fork be n. Since 5 beats/sec are produced, frequency of the sonometer wire will be (n+5) or (n-5).
Therefore,
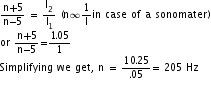
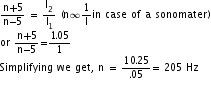
Q12. A source of sound produces waves of wavelength 28 cm. The source is moving with velocity 12 m/s due east. Find the apparent wavelength of wave received by observer on (i) east (ii) west of source. Take velocity of sound in air 336 m/s.
Solution
Here 

Q13. A large auditorium has a curved back. Why?
Solution
This is done to render the sound waves parallel so that these can be heard over a large distance. The speaker is placed at the focus of curved surface and the sound after reflection from curved surface becomes parallel.
Q14. The apparent frequency of the whistle of an engine changes in the ratio 3 : 2 as the engine passes a stationary observer. If the velocity of sound is 330 m/s, calculate the velocity of the engine.
Solution
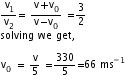
Q15. An observer at rest is standing near the train which blows the signal of frequency 400 Hz. Another train is approaching the observer with velocity 5m/sec which also blows the signal with frequency 400 Hz. If the observer hears 6 beatsin one second then what is the velocity of sound?
Solution
The apparent frequency of signal from train approaching towards observer is given by


Q16. Define transverse wave motion. What are the essential conditions required for the formation of transverse wave motion?
Solution
In a transverse wave motion, the particles of the medium through which the wave is travelling, vibrate in a direction perpendicular to the direction of propagation of the wave.
In the figure, the wave is travelling from left to right. (i.e., horizontally), whereas the particle vibrates simple harmonically in a vertical direction.
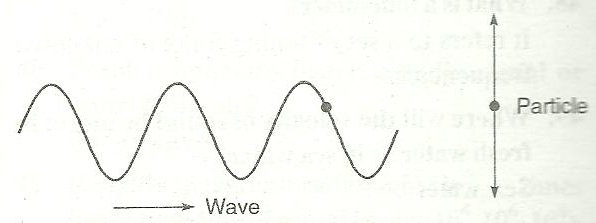 The essential conditions required in the medium for their propagation are :
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
The essential conditions required in the medium for their propagation are :
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
 The essential conditions required in the medium for their propagation are :
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
The essential conditions required in the medium for their propagation are :
(i) elasticity
(ii) inertia
(iii) absence of frictional resistance.
Q17. What is the difference between interference and beats?
Solution
Interference pattern is produced when two waves of same frequency travelling in same direction superimpose, while beats are formed when frequencies are slightly different.
In interference, the position of maximum and minimum are permanent i.e., intensity at a given point does not change with time, but in beats the intensity of wave changes at given point with time.
Q18. If the length of an open end organ pipe is doubled, what changes in its fundamental frequency will occur?
Solution
Fundamental frequency of the open end pipe, n = v/2L.
When the length is doubled,
n' = v/4L = n/2
Thus, the fundamental frequency is halved.
Q19. Obtain an expression for the apparent frequency of a note heard by an observer when,
(a) source alone is in motion towards the observer.
(b) source alone is in motion away from the observer.
(c) observer alone is in motion towards the observer.
(d) observer alone is in motion away from the observer.
(e) when the source and observer are moving towards each other.
Solution
(a) When source alone is in motion towards an observer:
The source (S) of sound is moving towards the stationary observer (O) with velocity, say us. Let n be the frequency of the sound waves. Thus, the source emits n waves per second. Let v be the velocity of the sound waves. If the source were at rest, n waves emitted by S would have occupied a distance v (figure) in one second. The first wave travels a distance v when nth wave is just emitted by S, as shown in the figure. True wavelength, 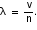 As the source has moved a distance us towards O, in one second n waves emitted by S will occupy a distance (v - us) as shown in the figure (ii). Therefore, the wavelength will be reduced. Let the reduced wavelength be
As the source has moved a distance us towards O, in one second n waves emitted by S will occupy a distance (v - us) as shown in the figure (ii). Therefore, the wavelength will be reduced. Let the reduced wavelength be 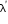 and apparent frequency n'.
Therefore,
and apparent frequency n'.
Therefore, 
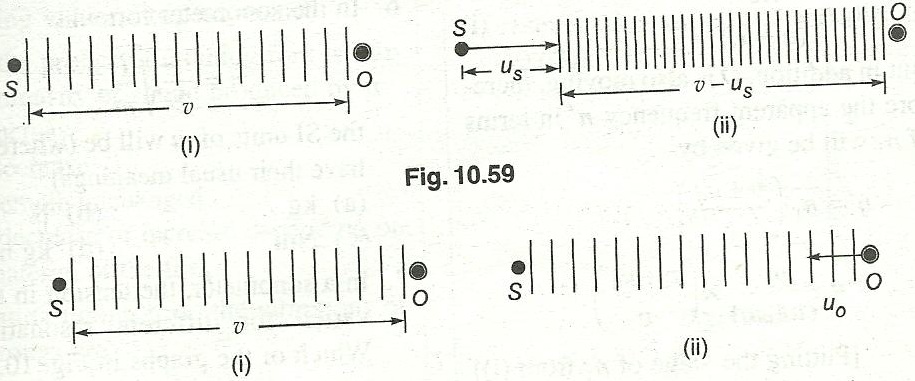
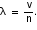 As the source has moved a distance us towards O, in one second n waves emitted by S will occupy a distance (v - us) as shown in the figure (ii). Therefore, the wavelength will be reduced. Let the reduced wavelength be
As the source has moved a distance us towards O, in one second n waves emitted by S will occupy a distance (v - us) as shown in the figure (ii). Therefore, the wavelength will be reduced. Let the reduced wavelength be 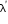 and apparent frequency n'.
Therefore,
and apparent frequency n'.
Therefore, 

Q20. If the frequency of a tuning fork is 400 Hz and the velocity of sound in air 320 m/s, find how far does the sound travel when the fork executes 30 vibrations?
Solution
v = 320 m/s, n = 400 Hz


Comments
Post a Comment