Q1. The average number of degree of freedom of an ideal gas molecules is five. The gas does 20J of work at constant pressure. Find the increase in internal energy and heat absorbed by gas.
Solution
The number of degree of freedom of gas f = 5
Therefore the value of 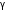 of gas is
of gas is 

Q2. Two vessels of the same size are at the same temperature. One of them holds 1 kg of H2 gas and other holds 1 kg of N2 gas.
(i) Which of the vessels contains more molecules?
(ii) Which of the vessels is under greater pressure and why?
(iii) In which vessel is the average molecular speed greater? How many times is it greater?
Solution
(i) Hydrogen. As 2 g of hydrogen contains N molecules, 1 kg of hydrogen contains N /2 x 1000 = 500 N molecules, where N = 6.023 x 1023. In case of N2, 28 g of nitrogen contains N molecules. Therefore, 1 kg of nitrogen contains N/28 x 1000 = 36N.
(ii) Hydrogen
As


Q3. The volume of a gas sample is increased. Why does the pressure, which is exerted by the gas, decrease?
Solution
As the volume of a gas is increased, its pressure decreases because of the fact that :
(i) The molecules have to travel a longer distance between impact on the walls of the container.
(ii) These impacts are now distributed over a larger area.
Q4. What do you mean by the number of degrees of freedom of a dynamical system? How many degrees of freedom are associated with
(i) a bob of an oscillating simple pendulum
(ii) an insect moving on a horizontal floor
(iii) a buzzing bee
(iv) a particle moving in a plane
Solution
The number of degrees of freedom of a dynamical system is defined as the total number of independent quantities required to completely describe the position and configuration of the system.
(i) one (ii) two (iii) three (iv) two
Q5. Calculate the root mean square velocity of oxygen molecules at 27oC. Take the density of oxygen to be 0.001424 g/cc.
Solution
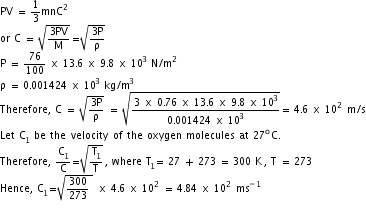
Q6. An electric bulb of volume 250 cm3 was sealed off during manufacture at the pressure of 10-3 mm of mercury at 27oC. Find the number of air molecules in the bulb.
Solution
Let n be the number of air molecules in the bulb.
Given : V1 = 250 cm3, P1 = 10-3 mm of Hg, T1 = 300 K
Using PV = nRT, where R is the universal gas constant, we get
10-3 x 250 = nR x 300 ...................(i)
At N.T.P, one molecule of air occupies a volume of 22400 cm3. So, at N.T.P,
V2 = 22400 cm3, P2 = 760 mm of Hg, T2 = 273 K, n2 = N = 6 x 1023 molecules
Therefore, 760 x 22400 = 6 x 1023 x R x 273 ......................(ii)
Dividing (i) by (ii), we get
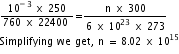
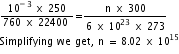
Q7. Using the law of equipartition of energy, calculate the total energy of one mole of monoatomic, diatomic and triatomic gases?
Solution
According to the law of equipartition of energy, the energy is equally distributed among all the degrees of freedom and that is equal to 1/2 kT. Therefore, if the degrees of freedom of gas molecules are f then internal energy of 1 mole of gas will be
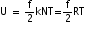 , where N is the Avogadro number.
Atomicity
Degrees of freedom
U
Monoatomic gas
3
, where N is the Avogadro number.
Atomicity
Degrees of freedom
U
Monoatomic gas
3
 Diatomic gas
5
Diatomic gas
5
 Angular triatomic gas
6
Angular triatomic gas
6
 Linear triatomic gas
7
Linear triatomic gas
7

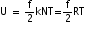 , where N is the Avogadro number.
Atomicity
Degrees of freedom
U
Monoatomic gas
3
, where N is the Avogadro number.
Atomicity
Degrees of freedom
U
Monoatomic gas
3
 Diatomic gas
5
Diatomic gas
5
 Angular triatomic gas
6
Angular triatomic gas
6
 Linear triatomic gas
7
Linear triatomic gas
7

Q8. The graph shows the variation of PV with P of given masses of three gases A, B and C. The temperature is kept constant. Which of these is ideal graph?


Solution
Gas C is ideal, because PV is constant for the gas. It means C obeys Boyle's law at all pressures.
Comments
Post a Comment